Misconceptions about OCR Bounding Boxes

Over the last year, I have been working on an application that auto-translates documents while maintaining the layout and formatting. It has many bells and whistles, from simple geometric tricks to sophisticated gen-AI algorithms and microservices. But basically, the app performs the simple task of identifying text in documents, machine-translating them, and reinserting them such that the output document “looks” like the input.

Most documents that my app has to process are PDFs. PDFs are ubiquitous but notoriously hard to analyze. Since pretty much every app is capable of producing a PDF file, its layout can get particularly nasty. Moreover there is no single semantic description of what comprises a document - e.g. an email is as much a document as a boarding pass. Who’s to say that a selfie is not a document? This means that my users can upload almost anything into the app, and as long as it has some text, it ought to be serviceable.

Obviously, OCR is a critical block of the pipeline. This post is about what I wrongly believed about OCR a year ago, and what I have grown to understand now, after having looked at hundreds of PDFs that come straight from a typesetter’s nightmare.

These are commonest misconceptions about OCR I’ve come across (even in my own work):

1. Words, lines and paragraphs have rectangular bounding boxes.
2. These rectangles have sides parallel to the X and Y axes.
3. They can be defined entirely by the top-left corner, the width and the height.
4. They are more horizontal than vertical.

Now, to be fair, these misconceptions aren’t outright disastrous. You can have them and still successfully process most of your input. Given that most documents are fairly clean, you’re likely to write your code based on this well-behaved subset. And that’s the way it should be, too. After all, you would want to cater to the norms first, not the exceptions.

The trouble is that when exceptions happen (and they will), they wreak havoc on your application. They are inevitable. And while it may be easy to get rid of these misconceptions¹, nothing beats not having them in the first place.

Let’s go over examples.

Bounding boxes are not necessarily rectangles

It’s reasonable to ask why we insist on bounding boxes being rectangular at all. There’s nothing wrong with quadrilaterals, after all. Rectangles are just ridiculously easy to manage across different kinds of media, and they are easier to store. If the OCR detects a perfect rectangle in a document, it’s easy to reproduce that rectangle very precisely in HTML as an SVG rectangle. Even in PDFs it’s easier to add rectangular annotations and text boxes. It’s not like SVG or PDF annotations can’t be polygons, but rectangles just fit.

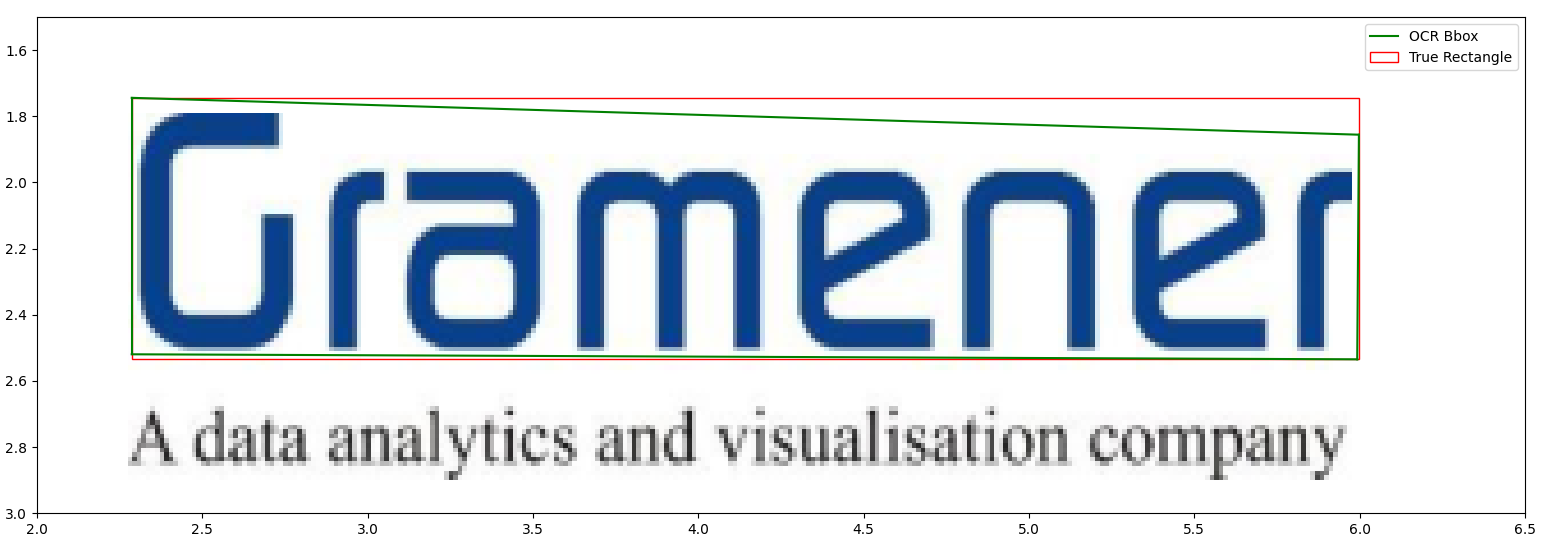
In this example, Azure FormRecognizer’s prebuilt-layout model (for consistency, all my observations in this post are based on the same model) predicts the green box.Note that it’s not a rectangle. FormRecognizer (and many other OCR tools) produce bounding boxes as an array of eight floats, i.e. an (x, y) tuple for each of the four corners. The red box is an approximation of the rectangle determined by finding the minimum and maximum of the x and y coordinates, respectively. Let’s call it the enclosing rectangle.

Notice that the top edge of the green polygon drops only about a fifth of an inch vertically over nearly four horizontal inches. So the deviation of the predicted rectangle from the true rectangle isn’t drastic. But if I wanted to determine the precise angle this word makes with the horizontal axis, I cannot use the green box. I have to then rely on the slopes of the top and the bottom edges of the enclosing rectangle.

So the seemingly obvious recipe is as follows: if the OCR doesn’t give you a perfect rectangle², find the minimum and maximum of the x and y coordinates.

Let’s now see how even this method can go wrong.

If boxes are rectangles, their sides need not be parallel to the axes

This effect is most apparent when locating rotated text in a document. In the example above, three sides of the enclosing rectangle - the bottom, left and right edges - coincide with the corresponding three sides of the predicted bounding box. But it’s quite common to have bounding boxes such that no side is parallel to either axis. This happens especially in photographs or scanned documents, when the camera is not aligned with the edges of the document.

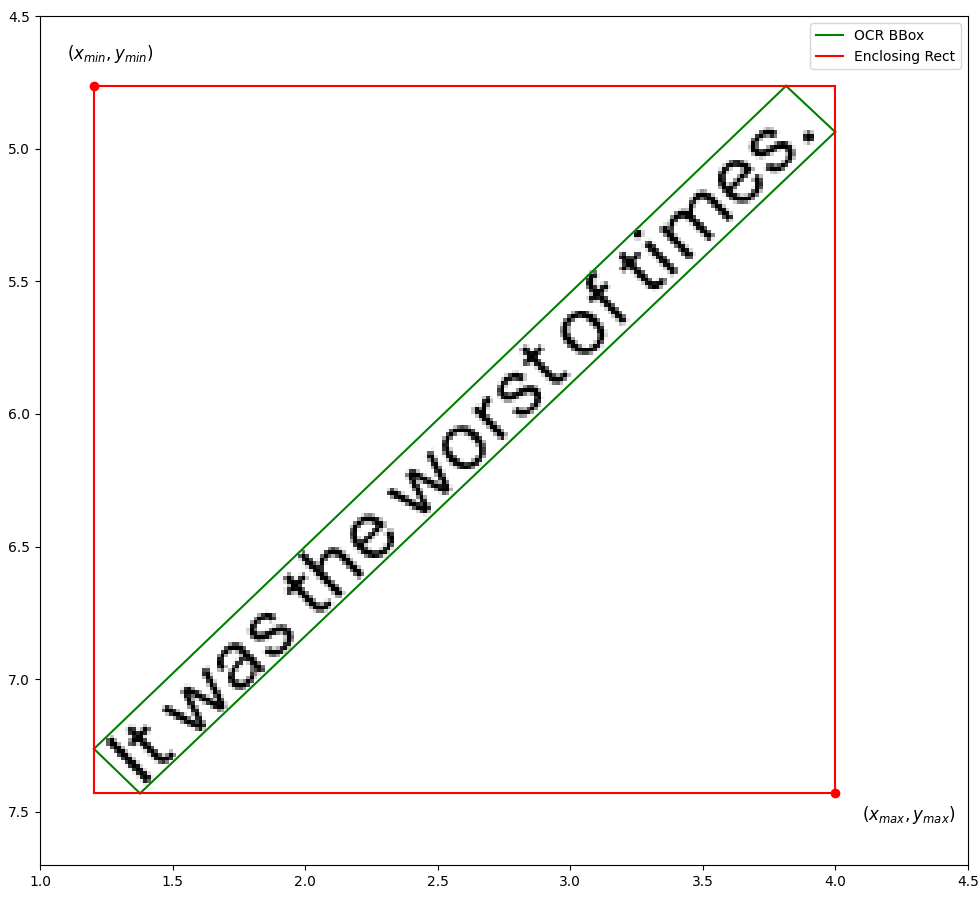
Let’s say the text makes an angle θ with the positive X axis. The deviation between the enclosing rectangle and the predicted bounding box worsens as θ gets farther from a multiple of 90 degrees. The figure above represents an extreme case where θ is 45 degrees. The enclosing rectangle is, as a result, unreasonably larger than the OCR bounding box.

Until I encountered the first rotated piece of text in my users’ documents, I had a 4-number system of storing bounding boxes - the x and y coordinates of the top left corner, the width and the height. This was convenient because I could directly use these four numbers to create all sorts of assets: an SVG rectangle, a matplotlib rectangle, and a PDF annotation too. But now I needed a fifth parameter, the angle which the text makes with the horizontal axis.

Even if boxes are rectangular, with sides parallel to the axes, their orientation is still ambiguous

Even if the previous misconceptions do not hold, i.e. even if the bounding box is perfectly rectangular and it’s sides are parallel to the axes, there’s still no guarantee that you get a well behaved bounding box.

Here’s the catch: text rotated at any non-zero multiple of 90 degrees will still have a perfectly rectangular bounding box. And if you’ve been using only a 4-tuple to define it, the angle of the text cannot be correctly found.

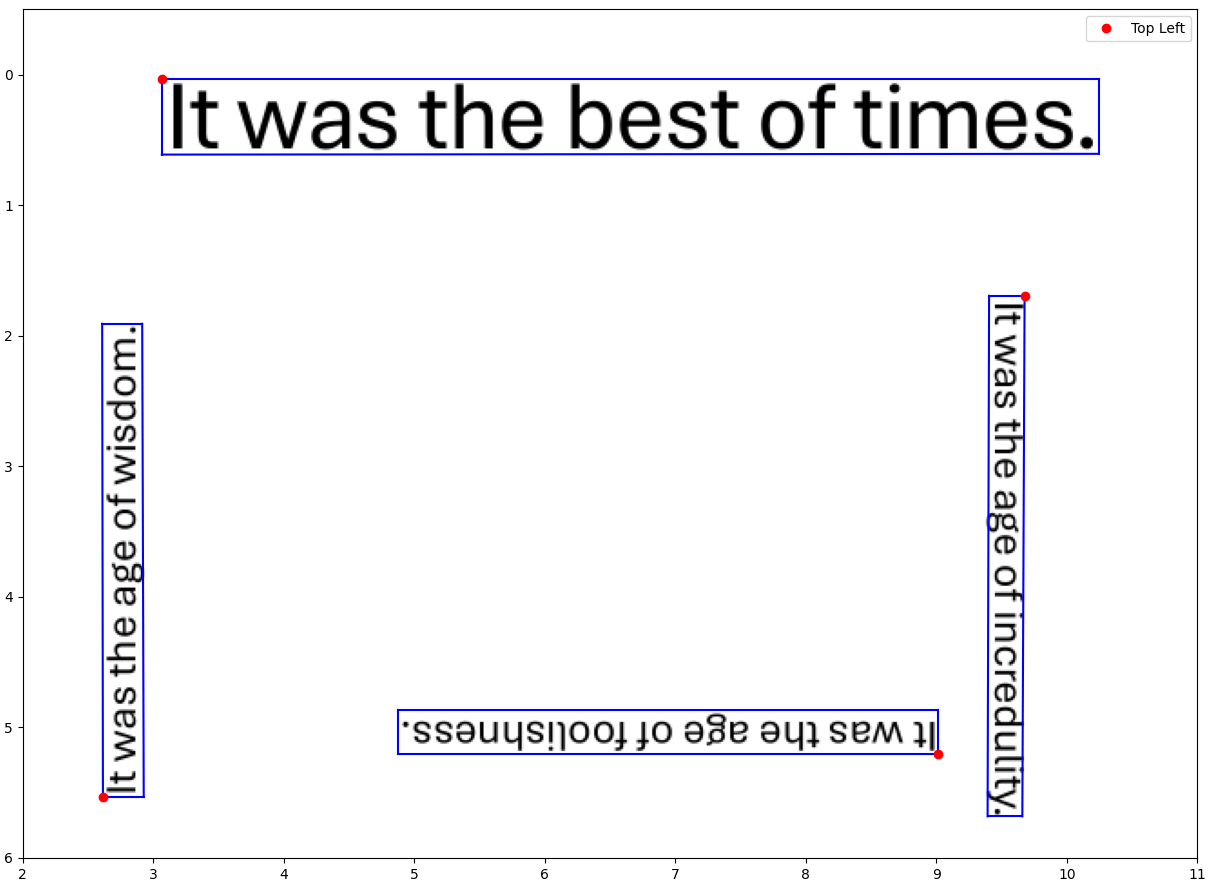
None of the four bounding boxes here have an odd angle. They’re all good rectangles, either vertical or horizontal. But as we can see, even for rotations that occur in multiples of 90 degrees, the adjectives “vertical” and “horizontal” can still be ambiguous. There are two vertical boxes, and two horizontal ones, making angles of 0, 90, 180 and 270 respectively with the horizontal axis.

If all we have is a 4-tuple system for defining bounding boxes, there is no way to infer these angles from them. This forces us to consider that (see the figure) the top-left corner of the bounding box can be any of the four vertices of the rectangle! It doesn’t necessarily have to be that vertex which is closest to the top left corner of the image itself.

To make matters worse, I often tend to forget that the Y axis is inverted - as is typical across multiple media like images, web pages and PDF files. I’ve lost count of how often I’ve painstakingly created rotation matrices, used them to transform the rectangles which ended up in the wrong place. And only later, with extreme exasperation, I’ve realized that the rotation was supposed to be clockwise instead of counter-clockwise - all because the Y-axis was inverted.

Vertical boxes don’t always have to be rotated

In the figure above, there are two boxes that are vertical. But both are rotated. If we were to de-rotate them, we’d end up with horizontal boxes, which are wider than taller. Nevertheless, it is possible that we get vertical bounding boxes, which are not rotated.

This misconception is more cultural than scientific. There exist many scripts, especially in South-East Asia where text is written from top to bottom. It is not uncommon in the Latin script either - signboards and advertisements can have English words written vertically.

This image shows a Vietnamese edict from 1765 written with Chinese characters. Formrecognizer correctly identifies the bounding boxes. In addition, their top-left corners are indeed those vertices that are closest to the origin of the XY plane.

It would be very easy to confuse these boxes with text that is actually horizontal, but rotated vertically, especially since we’ve seen multiple examples of such cases in the previous section.

What can we do about it?

It’s still helpful to remember that most documents you’re likely to encounter are:

1. going to be in English (or at least in a language that’s written with the Roman script)
2. likely to have been generated by a document processor.

As such, most documents you see will be pretty well formatted. It is the exceptions that we are concerned with. And when the exceptions come knocking, you better have left room in your code to handle them.

In summary, here’s what should be done:

1. If bounding boxes are not rectangular, approximate them such that the corners of the estimated rectangle are as close as possible to the corners of the original box (in the mean-squared-error³ sense).
2. Do not approximate rectangles by taking the minimum and maximum values of the x and y coordinates of the corners. See the second figure for an example of how this can go wrong.
3. Use at least 5 numbers for defining rectangle, the (x, y) coordinates of the top-left corner (the true top-left from the perspective of the text, not the one that’s closest to the origin), the width, the height and the angle that any fixed side makes with the X-axis.
4. Be careful about which bounding boxes need to be de-rotated.

If you’d like to learn more about how to comprehensive layout analysis with tools like Azure FormRecognizer, drop a comment below.

Acknowledgements: Many thanks to Harshad Saykhedkar and Dhruv Gupta for reviewing drafts of this post.